Kalkulatory granic to zaawansowane narzędzia online służące do obliczania granic funkcji matematycznych. Pozwalają na szybkie i precyzyjne wyznaczanie wartości granicznych dla różnych typów funkcji. Użytkownicy mogą wprowadzać własne funkcje i otrzymywać natychmiastowe wyniki obliczeń.
Narzędzia te wspierają analizę matematyczną na różnych poziomach edukacji. Obsługują funkcje wielomianowe, trygonometryczne, logarytmiczne i wykładnicze. Umożliwiają obliczanie granic lewostronnych, prawostronnych oraz obustronnych w dowolnych punktach.
Najważniejsze informacje:- Błyskawiczne obliczenia granic funkcji bez znajomości skomplikowanych wzorów
- Możliwość sprawdzenia granic dla wszystkich podstawowych typów funkcji matematycznych
- Wsparcie w nauce i nauczaniu analizy matematycznej
- Prezentacja kroków obliczeniowych ułatwiająca zrozumienie tematu
- Możliwość porównania własnych obliczeń z wynikami kalkulatora
- Dostępność różnych typów granic: lewostronna, prawostronna, obustronna
Jak działają kalkulatory do obliczania granic ciągów?
Kalkulator granic ciągów online to specjalistyczne narzędzie matematyczne, które automatyzuje proces obliczania wartości granicznych. Ten kalkulator granic pozwala na szybką analizę różnych typów ciągów i funkcji matematycznych. Obliczanie granic matematycznych staje się proste dzięki intuicyjnemu interfejsowi, który prowadzi użytkownika przez kolejne etapy. Narzędzie automatycznie wykrywa rodzaj wprowadzonego ciągu i dobiera odpowiednie metody obliczeniowe. System weryfikuje poprawność wprowadzonych danych i sygnalizuje potencjalne błędy.
- Automatyczne wykrywanie typu ciągu i dobór metody obliczeniowej
- Obsługa granic jednostronnych i obustronnych
- Szczegółowe wyjaśnienie kroków obliczeniowych
- Możliwość zapisywania i porównywania wyników
Prosty przewodnik używania kalkulatora granic
Obliczanie granicy funkcji online wymaga odpowiedniego przygotowania danych wejściowych. Zapoznaj się z krokami, które przeprowadzą Cię przez cały proces.
| Krok 1 | Wybór typu granicy (jednostronna/obustronna) |
| Krok 2 | Wprowadzenie wzoru funkcji lub ciągu |
| Krok 3 | Określenie punktu granicznego |
| Krok 4 | Weryfikacja poprawności danych |
| Krok 5 | Uruchomienie obliczeń i analiza wyniku |
Jakie rodzaje ciągów można obliczać?
Kalkulator granic obsługuje szeroki zakres ciągów matematycznych. Podstawowe typy obejmują ciągi arytmetyczne i geometryczne. Narzędzie do liczenia granic radzi sobie również z bardziej złożonymi przypadkami.
Szczególnie przydatne jest obliczanie granic matematycznych dla funkcji niewymiernych i wykładniczych. System automatycznie dobiera odpowiednie metody obliczeniowe, w tym regułę de L'Hospitala.
Zaawansowane algorytmy pozwalają na analizę ciągów rekurencyjnych. Kalkulator granic wielomianów szczególnie dobrze sprawdza się przy funkcjach wymiernych.
- Ciągi arytmetyczne (np. an = 2n + 1)
- Ciągi geometryczne (np. an = 2^n)
- Ciągi rekurencyjne (np. an+1 = an/2)
- Funkcje wymierne (np. (x^2-1)/(x-1))
- Funkcje niewymiernie (np. sqrt(x^2+1))
- Funkcje trygonometryczne (np. sin(1/x))
Ciągi specjalne i ich obliczanie
Niektóre ciągi wymagają szczególnego podejścia obliczeniowego. Kalkulator granic ciągów online wykorzystuje specjalne algorytmy dla funkcji z nieciągłościami.
W przypadku granic niewłaściwych system automatycznie stosuje odpowiednie przekształcenia. System analizuje zbieżność i rozbieżność ciągów.
Praktyczne przykłady obliczeń w kalkulatorze
Obliczanie granicy funkcji online najlepiej zrozumieć na konkretnych przykładach. Przyjrzyjmy się trzem typowym przypadkom.
Przykład 1: Granica funkcji wymiernej (x^2-1)/(x-1) gdy x→1 - Wprowadź funkcję w formie (x^2-1)/(x-1) - Określ punkt x=1 - Kalkulator wykryje nieoznaczoność typu 0/0 i zastosuje rozkład wielomianu
Przykład 2: Granica ciągu geometrycznego an = (1/2)^n gdy n→∞ - Wpisz ciąg jako (1/2)^n - Ustaw punkt graniczny jako nieskończoność - System automatycznie sprawdzi warunek zbieżności
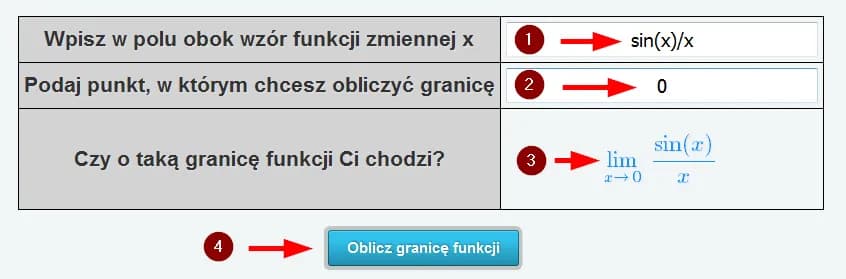
Przykład 3: Granica funkcji trygonometrycznej sin(x)/x gdy x→0 - Wprowadź funkcję sin(x)/x - Wybierz granicę obustronną w punkcie x=0 - Kalkulator zastosuje odpowiednie twierdzenia graniczne
Interpretacja wyników z kalkulatora
Kalkulator granic ciągów online przedstawia wyniki w przejrzystej formie numerycznej i symbolicznej. Wartości graniczne są wyświetlane wraz z dodatkowymi informacjami o zbieżności. System wskazuje też, czy granica jest właściwa czy niewłaściwa.
Przy granicach niewłaściwych narzędzie do liczenia granic pokazuje odpowiednie symbole nieskończoności. W przypadku granic jednostronnych wyniki zawierają oznaczenia kierunku granicy.
Szczególnie istotna jest interpretacja przypadków osobliwych. Obliczanie granic matematycznych może prowadzić do różnych typów nieoznaczoności, które kalkulator odpowiednio sygnalizuje.
| Wynik | Interpretacja |
| ±∞ | Granica niewłaściwa w nieskończoności |
| DNE | Granica nie istnieje |
| 0/0 | Nieoznaczoność wymagająca przekształceń |
| L± | Granica jednostronna (lewo/prawostronna) |
Na co uważać przy obliczaniu granic?
Kalkulator granic wymaga szczególnej uwagi przy wprowadzaniu danych. Najczęstsze problemy dotyczą niepoprawnej składni funkcji i błędnego określenia punktu granicznego.
Szczególną ostrożność należy zachować przy funkcjach zawierających pierwiastki i logarytmy. System może wymagać dodatkowej weryfikacji dziedziny funkcji.
W przypadku funkcji złożonych warto rozbić obliczenia na etapy. Pozwoli to na lepszą kontrolę procesu i weryfikację wyników pośrednich.
Przy granicach jednostronnych kluczowe jest prawidłowe określenie kierunku. Należy zwrócić uwagę na różnice między granicami lewo- i prawostronnymi.
System może potrzebować dodatkowych informacji przy niektórych typach nieoznaczoności. Warto wtedy skorzystać z wbudowanych narzędzi pomocniczych.
Ograniczenia kalkulatorów online
Kalkulator granic ciągów online może mieć trudności z bardzo złożonymi funkcjami. Szczególnie problematyczne są funkcje zawierające wielokrotne złożenia i nietypowe operatory.
W przypadku skomplikowanych ciągów rekurencyjnych, narzędzie do liczenia granic może wymagać dodatkowych przekształceń. System ma ograniczoną możliwość analizy ciągów zdefiniowanych indukcyjnie.
Niektóre kalkulatory granic mają limit długości wprowadzanego wyrażenia. Dotyczy to zwłaszcza funkcji z wieloma zmiennymi i parametrami.
Przy obliczaniu granic funkcji okresowych, wyniki mogą wymagać dodatkowej weryfikacji. System może nie wykryć wszystkich przypadków okresowości.
W sytuacjach wymagających zaawansowanych przekształceń algebraicznych warto rozważyć alternatywne metody. Można skorzystać z profesjonalnego oprogramowania matematycznego.
Pomocne może być również skonsultowanie wyników z innymi narzędziami obliczeniowymi. Warto porównać rezultaty z różnych kalkulatorów.

Gdzie znaleźć sprawdzone kalkulatory online?
Najlepsze kalkulatory granic znajdziesz na stronach uczelni i portalach edukacyjnych. Te narzędzia są regularnie aktualizowane i sprawdzane przez ekspertów.
Popularne platformy matematyczne oferują zaawansowane kalkulatory granic ciągów online. Często zawierają one dodatkowe funkcje edukacyjne i przykłady.
Warto zwrócić uwagę na narzędzia z możliwością generowania szczegółowych rozwiązań. Obliczanie granicy funkcji online staje się bardziej efektywne z dokładnym opisem kroków.
Przy wyborze kalkulatora zwróć uwagę na intuicyjność interfejsu. Narzędzie powinno oferować jasne instrukcje i pomoc kontekstową.
Istotna jest również możliwość eksportu wyników i zapisywania historii obliczeń. Dobry kalkulator umożliwia łatwe współdzielenie rezultatów.
Skuteczne wykorzystanie kalkulatorów granic - kluczowe wnioski
Kalkulator granic ciągów online znacząco upraszcza proces obliczania wartości granicznych w matematyce. Narzędzie to obsługuje szeroki zakres funkcji - od prostych wielomianów po złożone funkcje trygonometryczne i wykładnicze. Najważniejszą zaletą jest automatyzacja obliczeń i szczegółowe wyjaśnienie każdego kroku.
Mimo zaawansowanych możliwości, obliczanie granic matematycznych wymaga od użytkownika podstawowej wiedzy i uwagi. Kluczowe jest prawidłowe wprowadzanie danych, wybór odpowiedniego typu granicy oraz weryfikacja otrzymanych wyników. Warto pamiętać o ograniczeniach narzędzi online i w razie potrzeby korzystać z alternatywnych metod obliczeniowych.
Wybierając kalkulator granic, warto skupić się na narzędziach oferujących przejrzysty interfejs i dokładne objaśnienia kroków obliczeniowych. Najlepsze kalkulatory pochodzą ze sprawdzonych źródeł edukacyjnych i są regularnie aktualizowane, co gwarantuje wiarygodność wyników i wsparcie w procesie nauki.